Introduction linear regression with gradient descent

This tutorial is a rough introduction into using gradient descent algorithms to estimate parameters (slope and intercept) for standard linear regressions, as an alternative to ordinary least squares (OLS) regression with a maximum likelihood estimator. To begin, I simulate data to perform a standard OLS regression with maximum likelihood using sums of squares. Once explained, I then demonstrate how to substitute gradient descent simply and interpret results.

library(tidyverse)

## -- Attaching packages --------------------------------------- tidyverse 1.3.1 --

## v ggplot2 3.3.5     v purrr   0.3.4
## v tibble  3.1.3     v dplyr   1.0.7
## v tidyr   1.1.3     v stringr 1.4.0
## v readr   2.0.1     v forcats 0.5.1

## Warning: package 'readr' was built under R version 4.1.1

## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

Ordinary Least Square Regression

Simulate data

Generate random data in which y is a noisy function of x

set.seed(123)

x <- runif(1000, -5, 5)
y <- x + rnorm(1000) + 3

Fit a linear model

lm <- lm( y ~ x ) # Ordinary Least Squares regression with General Linear Model 
mod <- print(lm)

## 
## Call:
## lm(formula = y ~ x)
## 
## Coefficients:
## (Intercept)            x  
##      3.0118       0.9942

mod

## 
## Call:
## lm(formula = y ~ x)
## 
## Coefficients:
## (Intercept)            x  
##      3.0118       0.9942

Plot the data and the model

plot(x,y, col = "grey80", main='Regression using lm()', xlim = c(-2, 5), ylim = c(0,10)); 
text(0, 8, paste("Intercept = ", round(mod$coefficients[1], 2), sep = ""));
text(4, 2, paste("Slope = ", round(mod$coefficients[2], 2), sep = ""));
abline(v = 0, col = "grey80"); # line for y-intercept
abline(h = mod$coefficients[1], col = "grey80") # plot horizontal line at intercept value
abline(a = mod$coefficients[1], b = mod$coefficients[2], col='blue', lwd=2) # use slope and intercept to plot best fit line

Calculate intercept and slope using sum of squares

x_bar <- mean(x) # calculate mean of independent variable
y_bar <- mean(y) # calculate mean of dependent variable

slope <- sum((x - x_bar)*(y - y_bar))/sum((x - x_bar)^2) # calculate sum of differences between x & y, and divide by sum of squares of x
slope

## [1] 0.9941662

intercept <- y_bar - (slope * x_bar) # calculate difference of y_bar across the linear predictor
intercept

## [1] 3.011774

Plot data using manually calculated parameters

plot(x,y, col = "grey80", main='Regression with manual calculations', xlim = c(-2, 5), ylim = c(0,10)); 
abline(a = intercept, b = slope, col='blue', lwd=2)

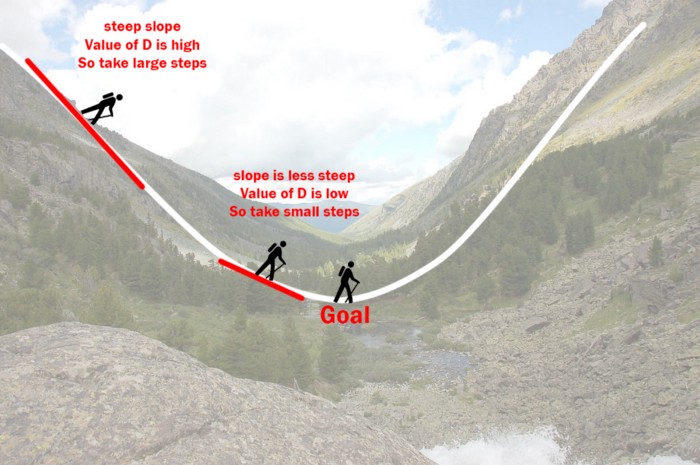
Gradient Descent:

Using the same simulated data as before, we will estimate parameters using a machine learning algorithm

Here’s some figures I found helpful while trying to understand how gradient descent works:

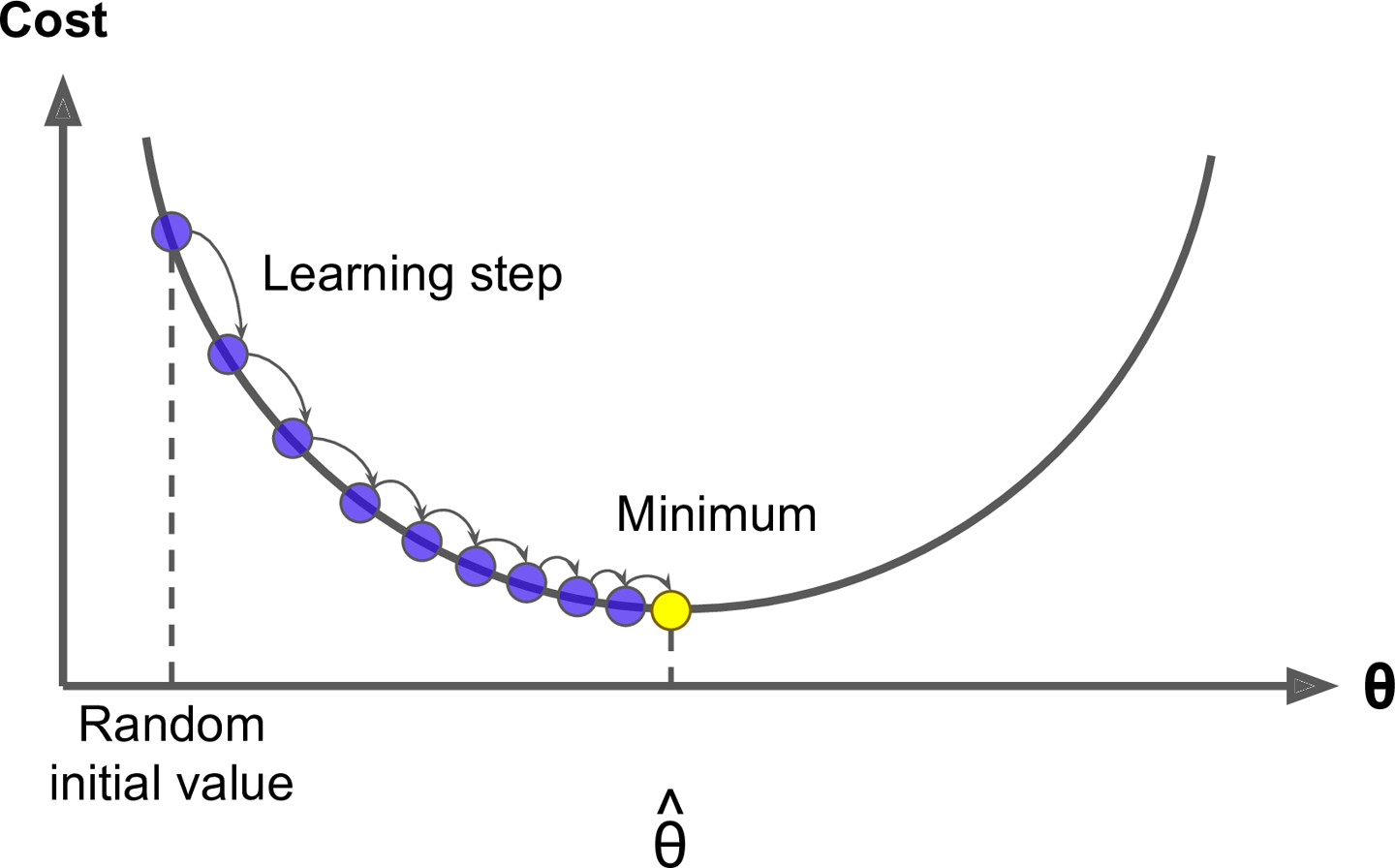
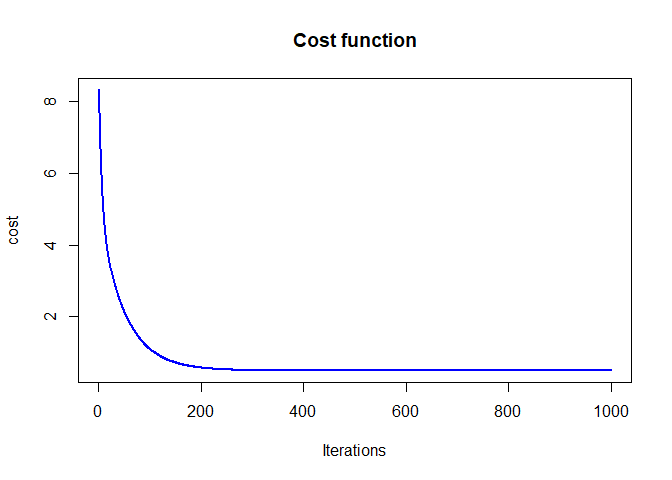
To determine the goodness of fit for a given set of parameters, we will empliment a Squared error cost function (a way to calculate the degree of error for a guess for slope and intercept)

cost <- function(X, y, theta) {
  sum( (X %*% theta - y)^2 ) / (2*length(y))
}

We must also set two additional parameters: learning rate and iteration limit

alpha <- 0.01
num_iters <- 1000

# keep history
cost_history <- double(num_iters)
theta_history <- list(num_iters)

# initialize coefficients
theta <- matrix(c(0,0), nrow=2)

# add a column of 1's for the intercept coefficient
X <- cbind(1, matrix(x))

# gradient descent
for (i in 1:num_iters) {
  error <- (X %*% theta - y)
  delta <- t(X) %*% error / length(y)
  theta <- theta - alpha * delta
  cost_history[i] <- cost(X, y, theta)
  theta_history[[i]] <- theta
}

print(theta)

##           [,1]
## [1,] 3.0116439
## [2,] 0.9941657

Plot data and converging fit

iters <- c((1:31)^2, 1000)
cols <- rev(terrain.colors(num_iters))
library(gifski)
png("frame%03d.png")
par(ask = FALSE)

for (i in iters) {
  plot(x,y, col="grey80", main='Linear regression using Gradient Descent')
  text(x = -3, y = 10, paste("slope = ", round(theta_history[[i]][2], 3), sep = " "), adj = 0)
  text(x = -3, y = 8, paste("intercept = ", round(theta_history[[i]][1], 3), sep = " "), adj = 0)
  abline(coef=theta_history[[i]], col=cols[i], lwd = 2)
}

dev.off()

## png 
##   2

png_files <- sprintf("frame%03d.png", 1:32)
gif_file <- gifski(png_files, delay = 0.1)
unlink(png_files)
utils::browseURL(gif_file)

Calculate intercept and slope using gradient descent (Machine Learning):

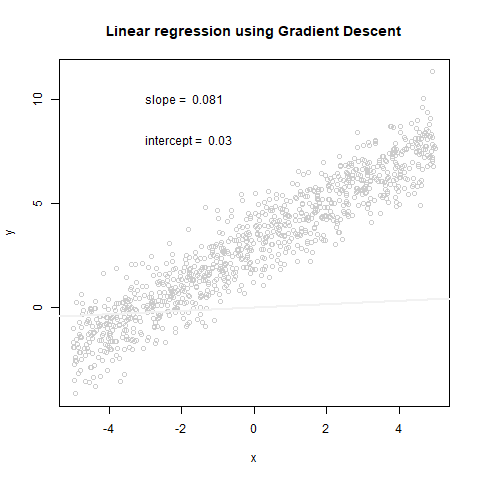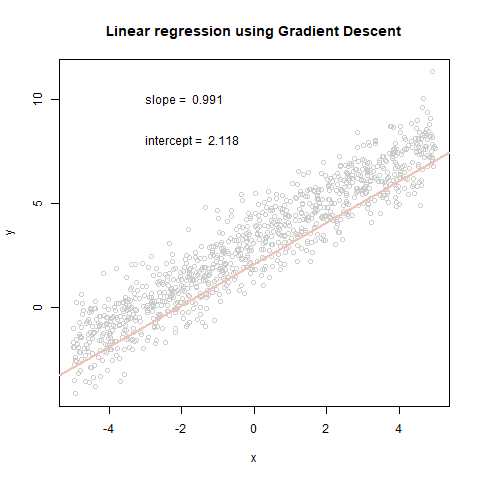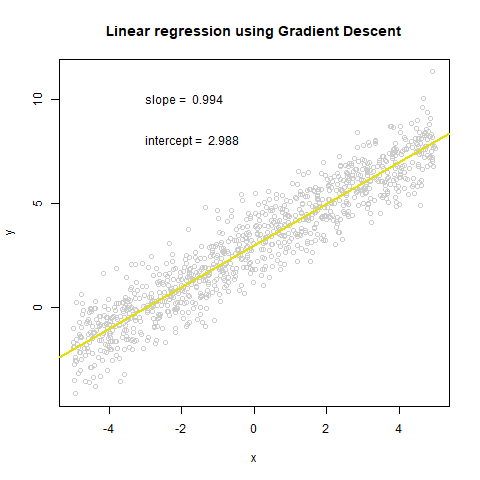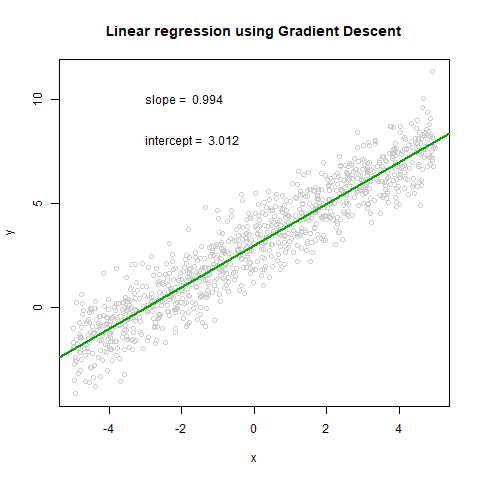
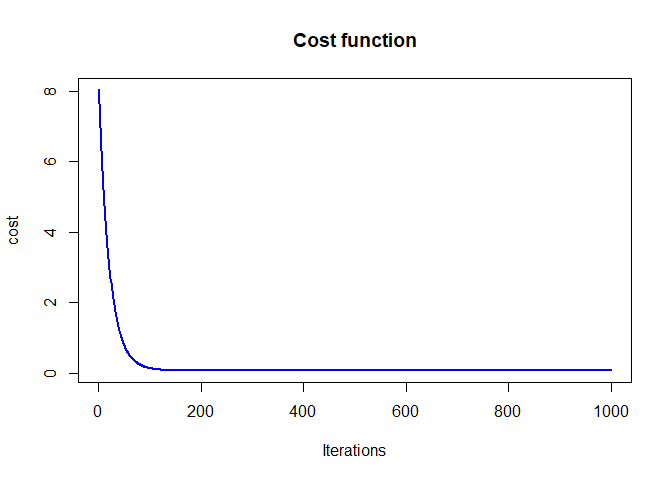
plot(cost_history, type='line', col='blue', lwd=2, main='Cost function', ylab='cost', xlab='Iterations')

## Warning in plot.xy(xy, type, ...): plot type 'line' will be truncated to first
## character

Using gradient descent with real data

I’ll demonstrate it’s features using an existing dataset from Bruno Oliveria: “Amphibio”:
• Link to publication: https://www.nature.com/articles/sdata2017123
• Link to data: https://ndownloader.figstatic.com/files/8828578

Load amphibio data!

install.packages("downloader")
library(downloader)

url <- "https://ndownloader.figstatic.com/files/8828578"
download(url, dest="lrgb/amphibio.zip", mode="wb") 
unzip("lrgb/amphibio.zip", exdir = "./lrgb")

df <- read_csv("AmphiBIO_v1.csv") %>%
  select("Order",
         "Body_mass_g",
         "Body_size_mm",
         "Size_at_maturity_min_mm",
         "Size_at_maturity_max_mm",
         "Litter_size_min_n",
         "Litter_size_max_n",
         "Reproductive_output_y") %>%
  na.omit %>%
  mutate_if(is.numeric, ~ log(.))

## Rows: 6776 Columns: 38

## -- Column specification --------------------------------------------------------
## Delimiter: ","
## chr  (6): id, Order, Family, Genus, Species, OBS
## dbl (31): Fos, Ter, Aqu, Arb, Leaves, Flowers, Seeds, Arthro, Vert, Diu, Noc...
## lgl  (1): Fruits

## 
## i Use `spec()` to retrieve the full column specification for this data.
## i Specify the column types or set `show_col_types = FALSE` to quiet this message.

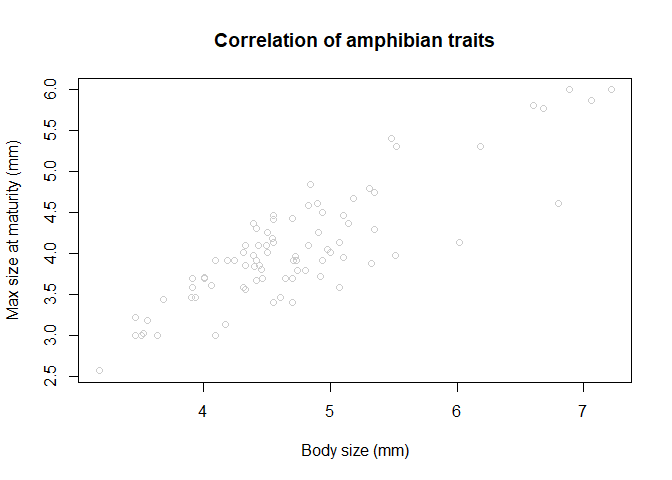
plot(df$Body_size_mm, df$Size_at_maturity_max_mm, col = "grey80", main='Correlation of amphibian traits', xlab = "Body size (mm)", ylab = "Max size at maturity (mm)"); 

Fit a linear model

lm <- lm(Size_at_maturity_max_mm ~ Body_size_mm, data = df) # Ordinary Least Squares regression with General Linear Model 
mod <- print(lm)

## 
## Call:
## lm(formula = Size_at_maturity_max_mm ~ Body_size_mm, data = df)
## 
## Coefficients:
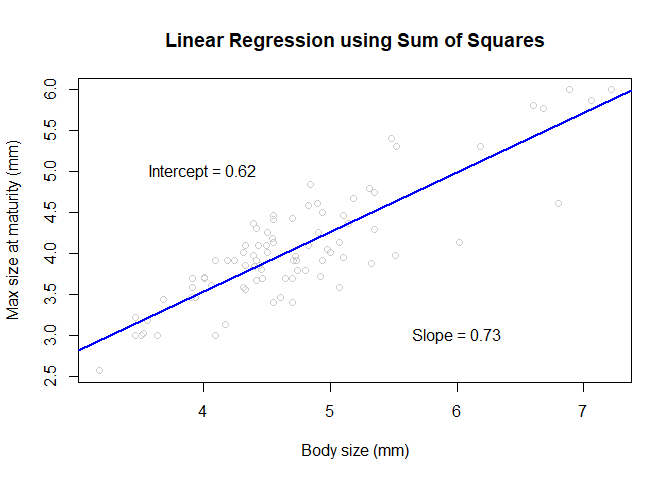
##  (Intercept)  Body_size_mm  
##       0.6237        0.7265

mod

## 
## Call:
## lm(formula = Size_at_maturity_max_mm ~ Body_size_mm, data = df)
## 
## Coefficients:
##  (Intercept)  Body_size_mm  
##       0.6237        0.7265

Plot the data and the model

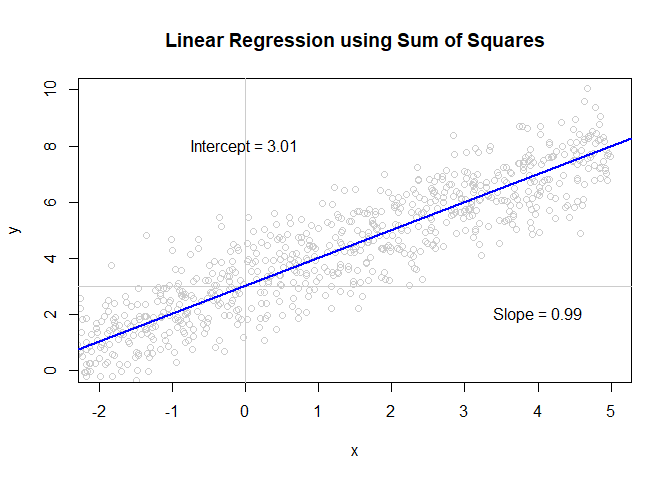
plot(df$Body_size_mm, df$Size_at_maturity_max_mm, col = "grey80", main='Linear Regression using Sum of Squares', xlab = "Body size (mm)", ylab = "Max size at maturity (mm)"); 
text(4, 5, paste("Intercept = ", round(mod$coefficients[1], 2), sep = ""));
text(6, 3, paste("Slope = ", round(mod$coefficients[2], 2), sep = ""));
abline(a = mod$coefficients[1], b = mod$coefficients[2], col='blue', lwd=2) # use slope and intercept to plot best fit line

Calculate intercept and slope using sum of squares

x <- df$Body_size_mm
y <- df$Size_at_maturity_max_mm
x_bar <- mean(x) # calculate mean of independent variable
y_bar <- mean(y) # calculate mean of dependent variable

slope <- sum((x - x_bar)*(y - y_bar))/sum((x - x_bar)^2) # calculate sum of differences between x & y, and divide by sum of squares of x
slope

## [1] 0.7264703

intercept <- y_bar - (slope * x_bar) # calculate difference of y_bar across the linear predictor
intercept

## [1] 0.6237047

### plot data using manually calculated parameters
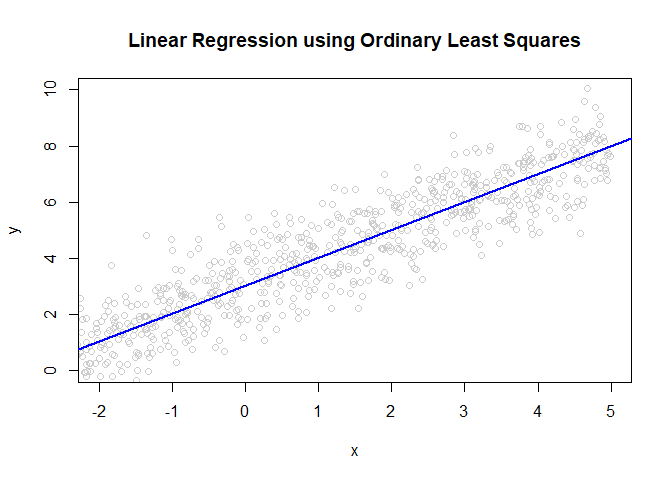
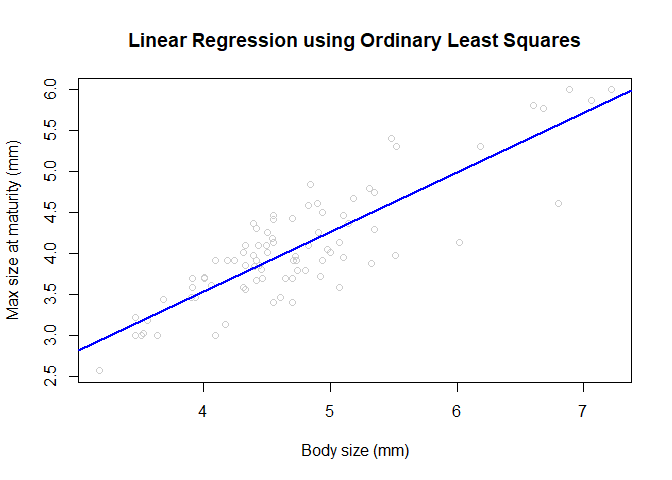
plot(x,y, col = "grey80", main='Linear Regression using Ordinary Least Squares', xlab = "Body size (mm)", ylab = "Max size at maturity (mm)"); 
abline(a = intercept, b = slope, col='blue', lwd=2)

Calculate intercept and slope using gradient descent (Machine Learning)

Squared error cost function (a way to calculate the degree of error for a guess for slope and intercept)

### learning rate and iteration limit
alpha <- 0.001
num_iters <- 1000

### keep history
cost_history <- double(num_iters)
theta_history <- list(num_iters)

### initialize coefficients
theta <- matrix(c(0,0), nrow=2)

### add a column of 1's for the intercept coefficient
X <- cbind(1, matrix(x))

# gradient descent
for (i in 1:num_iters) {
  error <- (X %*% theta - y)
  delta <- t(X) %*% error / length(y)
  theta <- theta - alpha * delta
  cost_history[i] <- cost(X, y, theta)
  theta_history[[i]] <- theta
}

print(theta)

##           [,1]
## [1,] 0.1816407
## [2,] 0.8175962

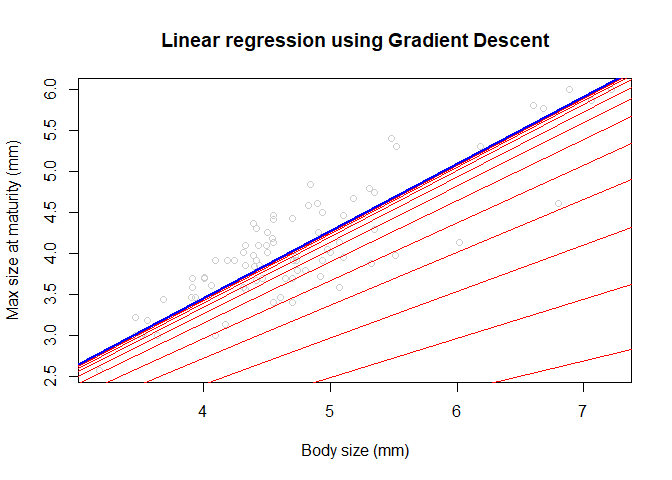
Plot data and converging fit

plot(x,y, col="grey80", main='Linear regression using Gradient Descent', xlab = "Body size (mm)", ylab = "Max size at maturity (mm)")
for (i in c((1:31)^2, 1000)) {
  abline(coef=theta_history[[i]], col="red")
}
abline(coef=theta, col="blue", lwd = 2)

plot(cost_history, type='line', col='blue', lwd=2, main='Cost function', ylab='cost', xlab='Iterations')

## Warning in plot.xy(xy, type, ...): plot type 'line' will be truncated to first
## character